【測量Excel】ATAN2で方位角0〜360°算出 北跨ぎ差分も解決

座標一覧表から、次の点への「方位角」を出したいだけなのに、Excel計算でハマっていませんか？

「普通のATAN関数を使ったら、南西の方角がおかしくなった」

「マイナスの角度が出てきて、360度表記にならない」

「北をまたぐとき（359°→1°）の計算で、進行方向の判定がエラーになる」

これらは測量や土木設計でExcelを使う際、誰もが一度は通る「魔の落とし穴」です。

要点だけ先に言います。測量座標の方位角計算に「ATAN」を使ってはいけません。「ATAN2」を使い、方位角（北=0°・時計回り）に合わせた補正をかけるのが実務の正解です。

この記事では、測量士や施工管理者が現場で即戦力として使える「方位角0〜360°算出の決定版」となる数式を紹介します。単なる数式の紹介だけでなく、ミスを防ぐための「検算セット」や、北跨ぎの差分判定まで、実務で必要な機能をまとめて扱います。

明日からの座標計算業務を、コピペ一発で安全運転に切り替えましょう。

コピペで完成する方位角の最終式

理屈や数学的な背景は後回しにして、「現場で今すぐ動く答え」を提示します。

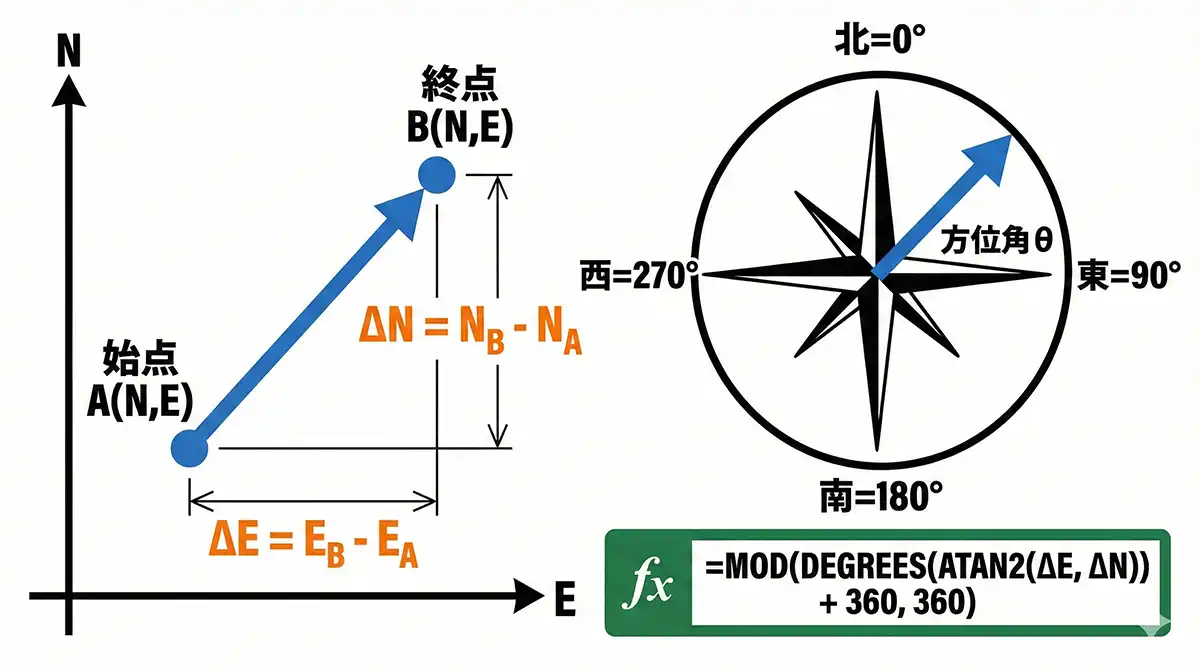
測量座標において、器械点（または始点）Aから、視準点（または終点）Bを見たときの「方位角（北＝0°、時計回り）」を求めるExcel数式は以下の通りです。

セルに貼り付けて、ΔNとΔEの部分を実際のセル参照に書き換えてください。

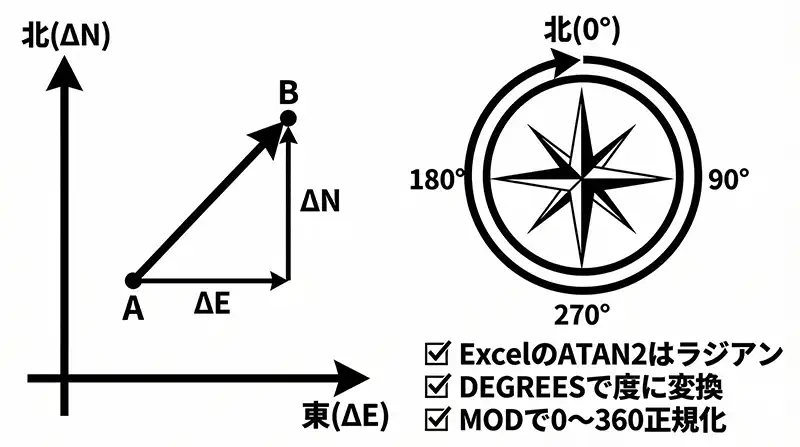
この式を使えば、計算結果がマイナスになったり、象限（北東・南西など）の判定ミスで値が狂うことはありません。

真北は0°、真東は90°、真南は180°、真西は270°として正確に算出されます。

変数の定義：ΔNとΔEの正体

数式の中にある「ΔN」と「ΔE」は、2点間の座標差分です。

ここでの最大の注意点は、引き算の順序です。逆にすると180度反対の方角が出てしまいます。

• ΔN（北方向の差） = 行き先（終点）のN座標 – 立点（始点）のN座標
• ΔE（東方向の差） = 行き先（終点）のE座標 – 立点（始点）のE座標

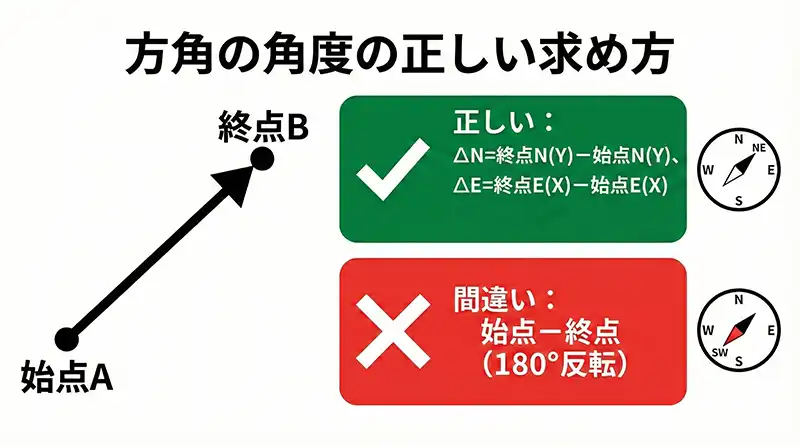
覚え方は「アトヒクマエ（後 引く 前）」です。

矢印の先（ターゲット）から、矢印の元（自分）を引くと覚えてください。

そのまま使えるExcel入力例

実務で座標計算書を作る際は、いきなり角度の列を作るのではなく、計算ミスを防ぐために「ΔN」「ΔE」の列を一度作ることを推奨します。

以下のような構成にしておけば、検算もしやすく、距離計算への流用もスムーズです。

列	項目	入力する数式・値
A	始点N（北）	100.000
B	始点E（東）	100.000
C	終点N（北）	150.000
D	終点E（東）	150.000
E	ΔN	=C2-A2
F	ΔE	=D2-B2
G	方位角	=MOD(DEGREES(ATAN2(F2, E2)) + 360, 360)

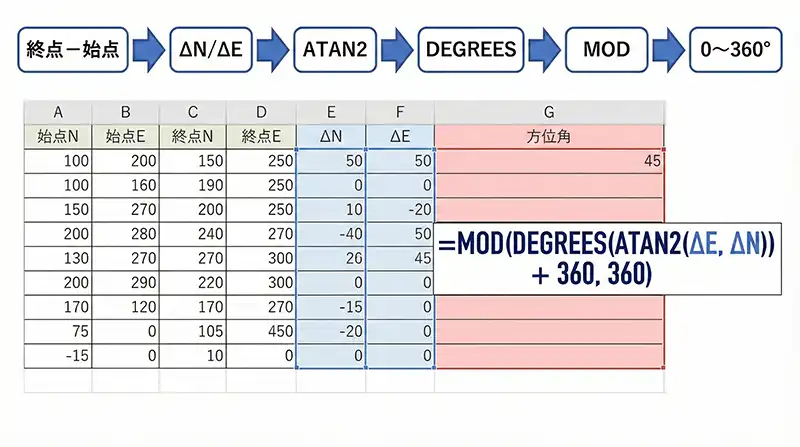
これで、G列に「45.000…」のような10進数の角度が表示されます。

「度分秒」表記が必要な場合は、Excelの表示形式ではなく、別の計算式で60進法へ変換する必要がありますが、まずはこの「10進数の正解値」が出せることが先決です。

つまずきポイントを潰して事故を止める

「数式を入れたのに、なぜか南西の方角だけ計算が合わない……」

これは私が現場で若手スタッフのExcelをチェックする際、最も多く遭遇するトラブルです。

測量の座標計算において、普通のATAN関数（アークタンジェント）を使うのは「事故のもと」です。

なぜATAN2でなければならないのか。現場で冷や汗をかかないために、3つの落とし穴を押さえておきましょう。

ATANで「象限ミス」が起きる理由

結論から言うと、通常のATAN関数は「北東（第1象限）」と「南西（第3象限）」の区別ができません。これが事故原因の代表格です。

理由は単純な算数のルールにあります。

ATAN関数は「縦÷横」の割り算の結果（傾き）から角度を求めますが、以下の計算結果を見てください。

 

• 南西へ進む場合（ΔN=-10, ΔE=-10）

  -10 ÷ -10 ＝ 1

 

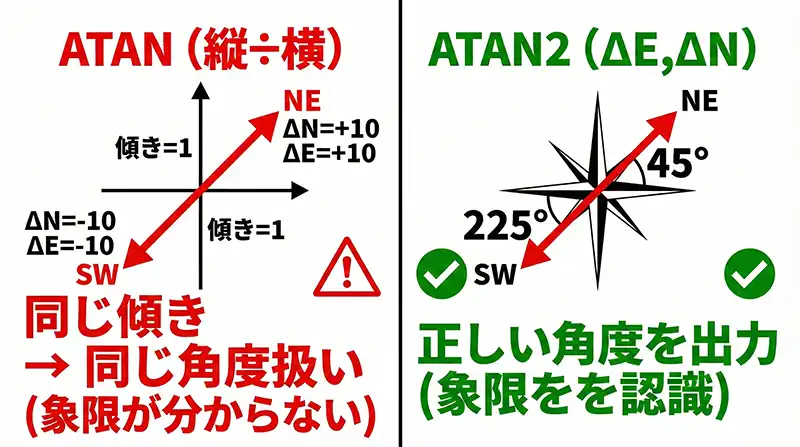
どちらも「1」になるため、Excelは「同じ角度だな」と判断して答えを返します。

実際、私が過去に修正した失敗例では、南西方向の擁壁ラインを計算しているはずが、すべて北東方向の座標として出力されていました。気づかずに丁張をかけていたらと思うとゾッとします。

ATAN2関数は、2つの値（ΔEとΔN）を「別々に」受け取ります。

「両方マイナスだから第3象限（南西）だ」と正しく判定できるのは、ATAN2だけなのです。

ラジアンを度に直す変換（0.785問題）

次に混乱しやすいのが、計算結果の意味不明な数値です。

Excelの三角関数は、我々が現場で使う「度（°）」ではなく、数学用の「ラジアン」で答えを返してきます。

• 我々の感覚：45°
• Excelの回答：0.78539…

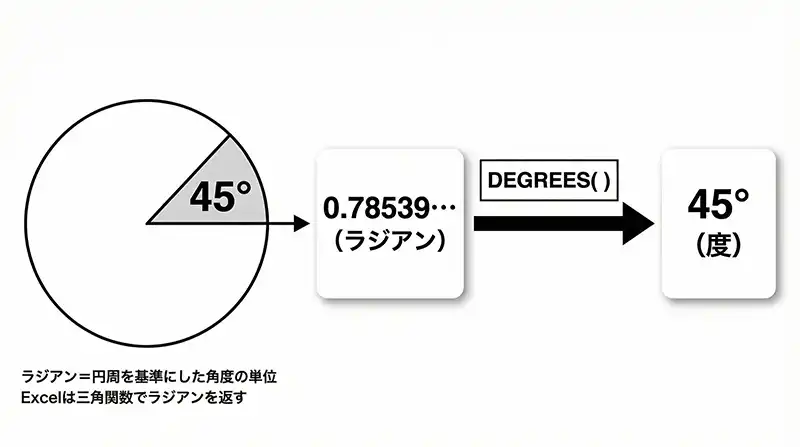
そのため、ATAN2の数式全体を DEGREES関数 で包み込み、強制的に「度」へ翻訳させる処理が必須です。

引数順で混乱しない覚え方（方位角は「E→N」）

最後にして最大のハマりポイントが、「カッコの中に入れる順番」です。

ここを間違うと、方位角が90度ズレたり、反転したりして計算結果が壊滅します。

ExcelのATAN2は ATAN2(y, x)（縦→横）という数学仕様です。

ただし、測量の方位角（北=0°・時計回り）を作るには、yにΔE（東西差）、xにΔN（南北差）を渡します。

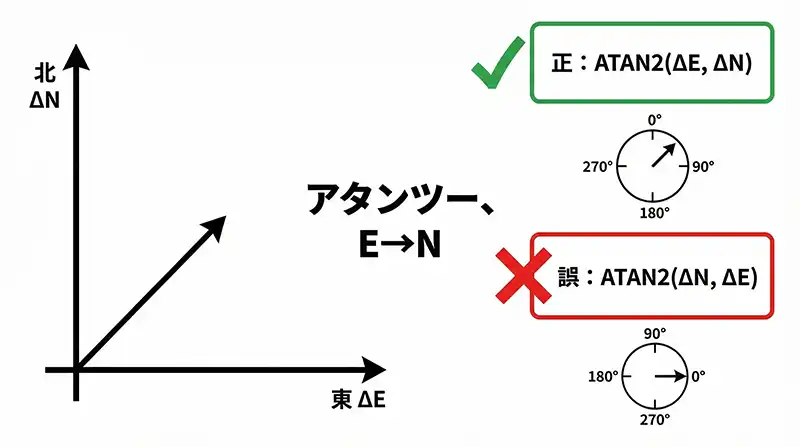
私は現場では、こう唱えて入力しています。

「アタンツー、E（東）→N（北）」

この順番さえ守れば、ATAN2は測量計算における最強の味方になってくれます。

次章では、入力した数式が本当に合っているか、現場投入前に確認する「鉄壁の検算セット」を紹介します。

検算セットで安心して運用開始する

数式を入力して「よし、できた！」とすぐに現場へ持ち出すのは危険です。

Excelの数式は目に見えません。もし参照セルが1つズレていたり、引数の順序（ΔE, ΔN）が逆だったとしても、Excelは涼しい顔で「間違った答え」を出し続けます。

測量の計算ミスは、手戻り工事や損害賠償に直結する重大な事故です。

コピペした数式が本当に正しいか、以下の「テストケース」で必ず検証してから実戦投入してください。

1. 東西南北の4方向チェック

基本の十字方向（0°, 90°, 180°, 270°）が正しく出るかを確認します。

あえて単純な数値（10と0）を入力し、計算結果が以下の通りになるかチェックしてください。

ケース	ΔN（北）	ΔE（東）	正解（度）	確認
真北	10	0	0°	□
真東	0	10	90°	□
真南	-10	0	180°	□
真西	0	-10	270°	□

2. 斜め4方向で「象限ズレ」を炙り出す

次に、ATAN（縦÷横）だと判定をミスりやすい「斜め方向」のチェックです。

ここさえクリアすれば、ATAN2関数が正常に機能している（＝符号による象限判定ができている）という確証が得られます。

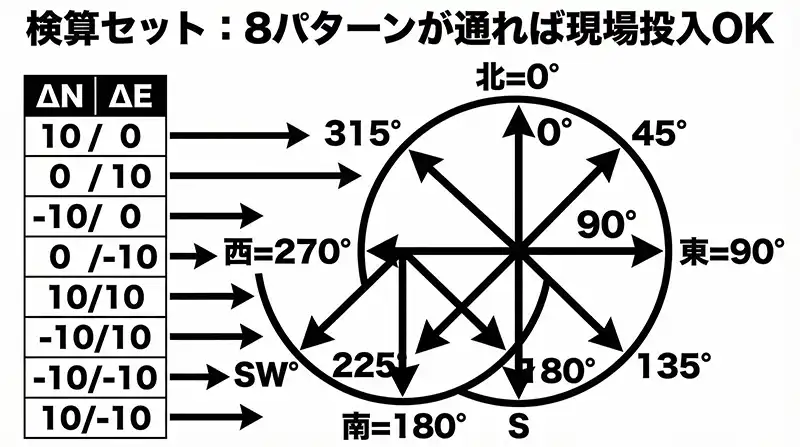
もし南西が 45° になっていたら、ATAN2の参照ミス（引数順や参照セル）を疑ってください。

この「8パターン検算」を通った計算シートなら、同僚や部下に渡しても事故は起きにくくなります。

3. 「同一点」という意外な落とし穴

実務では稀ですが、Excel操作のミスとして「始点と終点に同じ測点を選んでしまう」ことがあります。

この時、ΔN=0、ΔE=0 となり、計算式の結果は定義できません。

エラー表示のまま印刷されると、チェック体制を疑われかねません。

「距離が0（移動していない）なら、方位は空白にする」というIF処理を噛ませておくのが、プロの仕事です。

※IF/エラー制御の深掘り記事は、ここに内部リンクを差し込めます（準備中）。

進行方向の変化を判定する

道路の線形計算や、車両・ドローンのルート解析などで、直近の2点から「右に曲がったか、左に曲がったか」を自動判定したい場面があります。

ここで単純に「今回の方位 － 前回の方位」という引き算をすると、北（0°）を跨ぐ瞬間に計算結果が破綻します。これが「北跨ぎ（0°境界）の落とし穴」です。

この章では、この北跨ぎ問題を解決し、常に「最短の曲がり角度（-180°〜+180°）」を算出するテクニックを解説します。

単純な引き算が失敗する理由

• ケースA（通常）：方位90°（東）から100°（少し南）へ変化

  100 – 90 = +10°（右へ10度） → 正解

 

• ケースB（北跨ぎ）：方位350°（北北西）から10°（北北東）へ変化

  10 – 350 = -340°（左へ340度旋回？） → 間違い

 

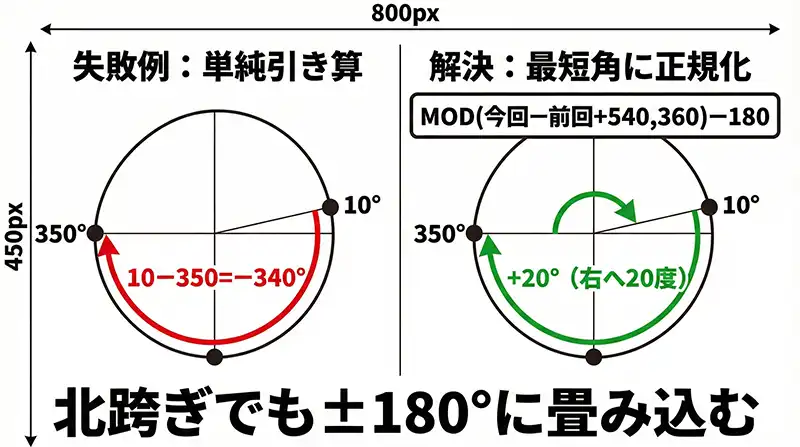
人間が見れば「右へ20度」と分かりますが、Excelは正直なので「左回りで340度回った」という計算結果を返してきます。これでは、その後の条件分岐（IF関数）が誤動作します。

最短角（-180°〜+180°）を出す数式

このズレを補正し、常に「近い方の曲がり角」を算出するには、以下の数式を使います。

この数式のポイントは、北を跨いでも必ず「±180度以内」に畳み込むことです。

右曲がりをプラス、左曲がりをマイナスとして扱えるので、判定ロジックが壊れません。

先ほどの失敗例（350°→10°）で検算してみます。

• 10 – 350 + 540 = 200
• MOD(200, 360) = 200
• 200 – 180 = +20°（右へ20度）

「直進・右折・左折」を閾値で判定する

方向差が出せたら次は「判定」です。

実務ではGPS誤差や施工誤差もあるため、閾値（しきいち）を設けるのが鉄則です。

例えば「±5度以内なら直進」とみなす場合、IF式は以下です。

=IF(ABS(方向差) <= 5, “直進”, IF(方向差 > 0, “右折”, “左折”))

表に組み込むと、台帳がこの形になります。

測点	方位角	方向差（補正後）	判定（閾値5°）
No.1	350°	–	–
No.2	352°	+2°	直進
No.3	10°	+18°	右折

実務で壊れない形に整える

ここまで解説した数式を使えば、計算結果としての「答え」は正しく出ます。

しかし、プロの仕事は「計算が合えば終わり」ではありません。

「半年後の自分」や「Excelが苦手な後任者」が見ても、一瞬で意味がわかる状態にしておくこと。

ここまでやって初めて、現場で運用できるツールになります。

「呪文」のような数式をLET関数で構造化する

Excel 2021以降またはMicrosoft 365なら、LET関数の採用を強く推奨します。

これを見て、すぐに「どっちがΔEで、どっちがΔNか」を判断できるでしょうか？

この「確認の手間」がミスを誘発します。

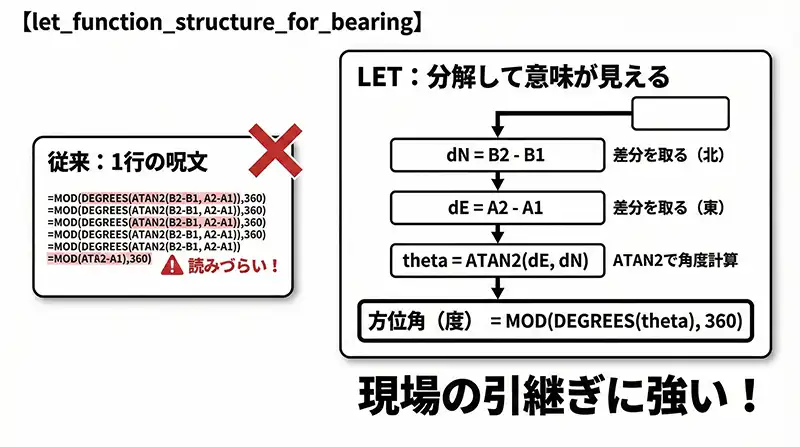
このように、数式の中で「dN」「dE」という変数（名前）を定義します。

誰が見ても「ここで座標差分を取っている」と分かる状態になるため、引継ぎ事故を潰せます。

「名前の定義」ではなくLETを使う理由

セルに名前をつける機能（名前の定義）でも似たことはできますが、測量・土木の現場では「名前の定義」は非推奨です。

• 名前の重複：シート複製のたびに警告が出やすい
• 参照範囲の事故：コピーしたのに、元シート参照が残ることがある

「コピペに強い」＝「現場に強い」という意味でも、LETが堅いです。

「移動していない」場合の例外処理を組み込む

物理的に「始点と終点が同じ座標（距離0）」の場合、方位角は定義できません。

そこで、「距離が0なら空欄」をLETの中に組み込みます。

連鎖する座標計算へ広げる

方位角が正確に出せるようになれば、そこを起点として実務で必要なデータも芋づる式に算出できます。

距離（S）をセットで算出する

測量の世界では、方向角（A）と距離（S）はセットです。

すでに算出してある ΔN と ΔE を利用すれば、平面距離はこの式で求まります。

360度を「方位名（文字）」に変換する

「135°」という数値は計算には便利ですが、報告書や打合せでは「南東」などの文字の方が伝わります。

これは VLOOKUP の近似一致（TRUE）で、テーブル参照として実装できます。

ラジアンと度（Deg）の関係を制する

三角関数で事故る原因の多くは「単位」です。

RADIANS／DEGREESの使い分けに不安がある場合は、角度計算の記事も合わせて確認しておくと、原因究明が早くなります。

→ ExcelのACOS関数を完全解説！初心者でもわかる角度計算の基本と応用

EXCELのACOS関数を完全解説！初心者でもわかる角度計算の基本と応用

「図面上の2本の線の角度を知りたい」「直角三角形の辺の長さから角度を逆算したい」そう思ってExcelで「=ARCCOS」と入力しても、関数の候補に出てこず困っていませんか？結論から言うと、ExcelにARCCOSという関数は存在しません。代...

zaiteku-banzai.com

2024.12.27

まとめ

測量座標における方位角計算は、ATAN2関数を使うことで堅牢に自動化できます。

1. 基本式：=MOD(DEGREES(ATAN2(ΔE, ΔN)) + 360, 360)
2. 注意点：Δは「終点 − 始点」。ATAN2の引数は (ΔE, ΔN)（方位角仕様）
3. 運用：同一点（0,0）はIFで空欄にする
4. 応用：方向の変化は最短角に正規化して北跨ぎを防ぐ

たった1つの数式ですが、これを知っているだけで現場での「座標が合わない！」というストレスから解放されます。

お手持ちの計算シートをアップデートして、事故の芽を潰していきましょう。